Theoretical Analysis of Specific Impulse at Lower Geo-Potential Altitude Range for a Paraffin-Fueled Hybrid Rocket Motor

Abstract

This paper presents a theoretical performance of paraffin-based hybrid rocket motors, focusing on the ideal specific impulse performance (Isp) at lower geo-potential atmospheric altitudes. The study considers n-docosane (C22H46) as fuel with oxidizer as nitrous oxide (N?O). Simplified mathematical modelling is employed to perform the analysis. The input thermodynamic parameters are calculated for exhaust gas mixture under balanced stoichiometric chemical reaction based on fixing a standardized exhaust temperature of 1000oK in relevance with material considerations. The analysis underscores the influence of specific heat capacity and specific heat ratio on thrust coefficients. The nozzle area ratio is fixed as 2.5 and accordingly the design exit Mach number (Me) is calculated using Chebyshev iterative method by formulating a transcendental non-linear function and accordingly theoretical computations are performed based on the methodology followed. The inference reveals that the ideal specific impulse ranges from 218 to 246 seconds across lower atmospheric geo-potential altitudes. This also highlights the influence of chamber pressure on altitude as a performance assessment for propulsion system. The findings are theoretical and delivers valuable insight into application of hybrid propulsion systems for altitude operations in future.

Introduction

I. INTRODUCTION

Hybrid rocket motors are emerging as a promising solution for sustainable and efficient space propulsion, combining the benefits of both liquid and solid based systems. The hybrid system delivers controllable thrust, enhanced safety, and reduced environmental impact, making them a cost-effective alternative for future missions [11]. As presented in Fig. 1, a layout of hybrid rocket motor includes a solid fuel and gas or liquid based oxidizer, simplifying design while improving performance and safety compared to traditional propulsion systems [1-2]. Their flexibility in thrust control and efficiency makes them ideal for applications ranging from small satellite launches to crewed missions [8].

A. Working Operation of Hybrid Propulsion System

Working of a hybrid rocketry unit involves the careful controlled delivery of sufficient oxidizer supply to the combustor unit where it mixes with the fuel resulting in high pressure gases which gets expelled through the exit nozzle section which is responsible for the pressure energy conversion to kinetic energy producing the forward propulsive force which is called as ‘Thrust’ [1-6]. Every part at the component level plays a critical function in maintaining efficient and effective operation in a hybrid rocket system as shown in the below Table 1 based on Fig. 1.

Table 1: Functions of each component

Fig. 1 :  Layout of a Hybrid Rocket Motor

B. The International Standard Atmosphere (ISA) Model

An international agreement is reached to refer to standardized atmospheric condition which are based on the average conditions existing at 40? N latitude at mean sea level & is known as the International Standard Atmosphere (ISA) [21]. This model is an important tool in assessing the performance of aerospace vehicles from sea level up to the different layers of atmosphere as shown in Fig. 2. The ISA helps to assess how aerospace vehicles respond to various atmospheric pressure and temperature during its flight [5, 24]. The Fig.2 shows the variation of temperature and pressure across different atmospheric layers [24]. The main layers context to this work is lower troposphere (0 to 12km) and lower stratosphere (12 to 50km) [24]. The upper atmosphere is heterogenous which is influenced by solar activity, seasons, and time of day. This study focuses on specific impulse (Isp) variations across the lower atmosphere (0–50 km) altitude regimes, where theoretical deviations are expected.

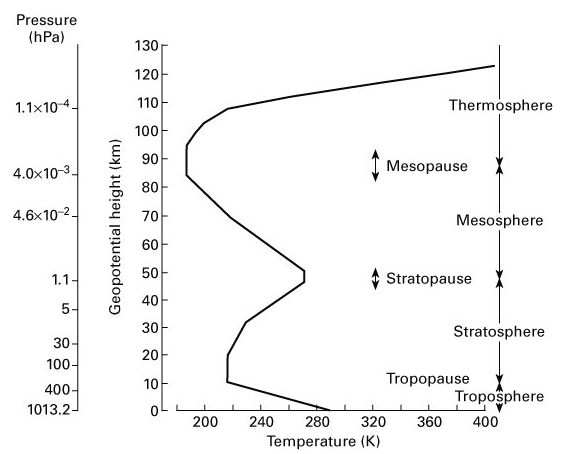
Fig. 2:  Structure of ISA Model as per ICAO  [24].

???????C. Specific Impulse and Fuel Selection 

Specific Impulse (Isp) is a critical parameter in assessing the performance of hybrid rocket systems, as it measures the efficiency of the propulsion system in converting propellant mass into thrust. Studying Isp across various altitude ranges allows for a comprehensive understanding of how performance varies with atmospheric conditions, ultimately guiding the design and operational strategies for hybrid rockets [1],[19-23]. In this study, paraffin wax variant n-docosane (C22H46) is selected as the economic fuel for hybrid rocket propulsion, paired with nitrous oxide (N2O) as the oxidizer. The selected paraffin wax variant offers a favourable balance of energy density, cost-effectiveness, and ease of handling as per the theoretical work carried out by Sreehari , et al., (2025) while N2O provides a reliable and efficient oxidizing agent based on the experimental work performed by Galfetti , et al.,(2013) and Tariffa,et al.,(2019)  reveals a promising combination for advancing hybrid rocket technology, particularly in the context of lower altitude operations [14-18],[19],[23-25]. Another perspective of using N2O is its non-toxicity characteristics and eco-friendliness makes as a sustainable oxidizing agent for fuel mixing.

II. METHODOLOGY FOR THEORETICAL COMPUTATION AND ANALYSIS

The below process chart Fig. 3 presents the methodology carried out for this theoretical study work to estimate the variation of Specific Impulse (Isp) with atmospheric geo-potential altititude ranges from 0 to 50 km. The height is typically considered as a geopotential height (h) in kms as per the ICAO standards for ISA model [24]. The importance of combining C22H46 with N2O is already specified on Section I-A. It’s important to analyze the balanced chemical equations to obtain the necessary thermodynamic parameter value based on the combustible products.

Fig. 3:   Methodology Flow Diagram

???????A. General Assumptions and Considerations for Mathematical Computation

The following assumptions and consideration are made to for performing the theoretical formulation and computation of performance parameters:

1. The reaction of the products is stable equilibrium with balanced stoichiometry maintaining a standard averaged temperature of 1000oK with regard to the material considerations also as per the simulation-based work performed by Migliorino, et al., (2019) at the nozzle for reasonable calculation of the thermodynamic parameters such as Gas Constant (R) and specific heat ratio (k) for the exhaust products when C22H46 reacts with N2O.
2. For the reduction of complexity of numerical modelling and computations, the multiphase effects of the products are not considered (For example water vapor is taken as the product of the reaction instead of water based on the temperature range) However, the stoichiometric balance of the reaction is carefully accounted for maintaining the level of accuracy for the results neglecting additional deposition of carbonated wax at the nozzle side linings.
3. The flow is isentropic with skin friction losses and nozzle divergence losses are neglected especially for the computation of Thrust Coefficient CF based on the work carried out by Parkinson, et al., (1981) [20].
4. As Isp(h) is in relation with the gravity field value g(h) is calculated at sea level taking the latitude value of the assumed launched location 13.7oN (Srihari Kota) as 9.7806 m/s2. This step of consideration is discussed in the further section of this work [26].
5. The atmospheric drag and solar radiation effects are neglected based on the geopotential height variation from seal level point to lower stratosphere range while calculating Isp(h).
6. To simplify the analysis and minimize additional uncertainties, the nozzle geometrical aspect and propellant flow rate and oxidizer-to-fuel ratio are not explicitly considered. This approach allows for a more focused evaluation of the thermodynamic properties without introducing complexities related to flow dynamics and mixture ratios while computing the Isp(h)

???????B. Stoichiometrically balanced chemical equations for finding k value

For a stable chemical equilibrium to occur the reaction need to be stoichiometrically balanced to yield the required products. The balanced chemical equation between n-docosane (C22H46) with oxidizer as nitrous oxide (N2O) shown in below chemical equation

C22H46 (s) + 67N2O(g) --------> 44 CO2 (s) + 46 H2O (g) + 67 N2(g)             (1)

As we observe in (1) the R.H.S side is having higher no of moles which increase the molecular weight in addition to the release of nitrogen gas (N2) based on the product formation the following required parameters are calculated based on the equations Based on work carried out by Sreehari, et al.,(2025) the below expressions are applied in finding out the value of k . The value of Gas constant for the product side is obtained as 

                                                       (2)

the unit of R is in J/kg-K and the Universal Gas Constant, Ru has a value of 8.314 J/mol-K.  the averaged molar mass of the products in (1). The total specific heat capacity CP Total is calculated depending on mole fraction ‘yi’ of the individual compounds of exhaust mixture with individual CPi values as mentioned in the below expression [7],[27],[14]. the unit is expressed in J/kg-K

 =                                                                         (3)

From (3) and (2) the specific heat ratio k for the mixture can be calculated accordingly using below thermodynamic relation  [1-8].

                                                                                         (4)

C. ???????Formulation of Transcendental Mach function f(Me) and Computation of  CF

The area ratio (ε) expression for the nozzle as shown below expression (5) [1-8].

                                                     (5)

here Me is the design exit Mach number and k is the ratio of specific heat obtained from (4) based on the work related to [14] processed a transcendental equation in terms of Mach number is formulated based on (5) is as follows with inputting the obtained value of k

                                             (6)

The above expression (6) can be solved using the Chebyshev numerical method as it yields faster convergence for such type of functions with minimal iterations. The work referred by Sreehari, et al.,(2025) based on the work in [21] pertained to Chebyshev algorithm or referred as ‘’Extended Newton Raphson’’ method is mathematically expressed as shown in below [9-10].

                                                (7 )  

Where Mei is the present guess value which is taken based on the consideration of nozzle chocking where Me=1 and the guess value is taken above the sonic value with guess interval [1.3,5) and accordingly iteration is carried out for the next iteration value Mei+1. The first and second derivative of the f(Me) and is denoted as f’(M(ei)) and f''(Mei+1 ) respectively. By iterating the above (7) with different initial guess values the value of Me can be obtained based on the tolerance of convergence of f(Me) may be from tolerance value of convergence from 10-9 to 0. A typical convergence curve is shown in Fig 4.

The theoretical analysis carried out by Bose, et al., (2012) presents the importance of thrust coefficient CF as performance parameter based on the selection of fuel and oxidizer resulting k values. The CF value shows the effectiveness of pressure at the chamber Pc which is converted into forward propulsive force which known as ‘Thrust’ (F).

Fig. 4:  Convergence curve for Chebyshev Method for  

The analysis performed by Parkinson, et al., (1981) explored a relationship using the pressure integral method for CF in terms of k and Me which is given in [20] and is shown in (8).

                                                       (8)

???????D. Mathematical Modelling for Calculating Theoretical Isp

Specific Impulse is a measure of performance efficiency attribute of an aerospace engine which consumes fuel to produce forward propulsive force ‘Thrust’ (F)which has the unit in Newton (N). In general, thrust equations can be expressed in (9). where C* and C is the characteristic velocity and effective exhaust velocity respectively having units in m/s or km/s for higher magnitudes.   is the propellent mass flow rate in kg/s. There is another term called ‘SPC’ called as the Specific Propellent Consumption in kg/N-s which shows the degree of thrust produced based upon given propellant flow rate . Lower value of SPC indicates higher performance of the vehicle.

                    (9)

Ve is the ideal exit velocity of the nozzle in m/s which contributes to the ‘momentum thrust’ to the rocket based on the velocity generated as a result of ejected gases from the exit nozzle. This is expressed as shown in (10) . The chamber and parameters are denoted with suffix ‘c’ and ‘e’ respectively. In consideration of material integrity and thermal properties the combustor and is maintained at a minimal temperature Tc of 2000oK but it may go beyond when advanced numerical analysis is performed upto 34000K based on the work carried out by Migliorino, et al., (2019). In practical sustaining the high heat value for any material is challenging [12-15]. The combustion chamber pressure Pc is varied from 2.0,8.0 and 15.0 MPa, accordingly Isp(h) is calculated for different geopotential altitude (h) values

 =                                                                                   (10)

The nozzle exit pressure Pe is calculated based on the below isentropic relationship [5]. The ambient pressure Pa is calculated based on the corresponding ISA values for ‘h as per (11).

                                                                                                 (11)

A convincing theoretical expression has been formulated for  as shown in (12) based on the earlier mathematical expressions provided by Sutton, et al., (1993) and Ramamurthi, et al., (2016) associated with the fundamentals of rocket performance [1-8]. Dimensional analysis is performed for the below expression and found to be consistent on both L.H.S and R.H.S

                                                                 (12)

In the expression (13)   is the acceleration due to gravity field [6]. The parameter ‘Φ’ which is the latittide angle associated with the location of reference launch site. In this context it is taken as 13.7oN (Sriharikota) accordingly the reference value is computed as 9.7806 m/s2 to maintain a practical relevance for the work [26]. The value may be different based on Φ here it is assumed as nearly constant with respect to altitude. Here in this context the g(h) is simply referred as ‘g’ in this context.

         (13)

III. RESULTS AND DISCUSSION

As per the methodology outlined in Section II-B to Section II-C, the following fixed input values have been determined as shown in Table 2 for conducting the theoretical analysis

Table  2: Calculated  Input Parameters for Ideal Specific Impulse Analysis

The analysis of theoretical Specific Impulse response across altitudes from the troposphere to the stratosphere, using sea level conditions at, h=0 as the reference which yielded the below inference,

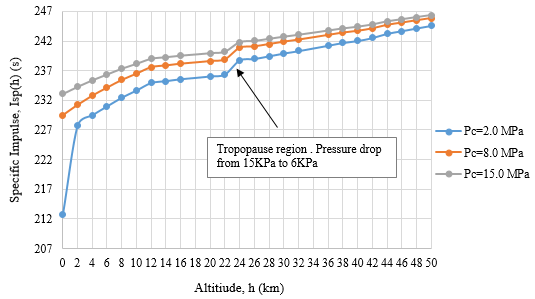
Fig. 5 : Effect of Geo-Potential Altitude on Specific Impulse

???????A. Variation of Isp(h) with Geo-potential altitude h

Specific impulse increases with altitude, primarily due to the decreasing ambient pressure. Notably, between 22 and 24 km, there is a sharp rise in Isp as the ambient pressure drops significantly from 15 kPa to 6 kPa, allowing the exhaust gases to expand more efficiently. The Fig. 5 highlights the critical role of altitude in optimizing rocket performance, where reduced atmospheric resistance enhances thrust potential. Based on the observation it is found that higher Pc is required for operating at increase altitude and this is due to the thinning atmosphere provides less resistance, allowing the high expansion of exhaust gases.

???????B. Variation of C and Ve with Isp(h)

In Fig. 6 it is inferred that, at lower altitudes and low chamber pressures, Specific Impulse increases with the ideal exit velocity exceeding the effective exhaust velocity as a result of incomplete nozzle expansion which validates the theoretical insights generated by Senthil, et al., (2009) [5]. At higher altitudes and higher chamber pressures, the effective exhaust velocity becomes greater than the ideal exit velocity because the nozzle expansion is at its optimal levels to meet thrust requirements with increasing chamber pressure.

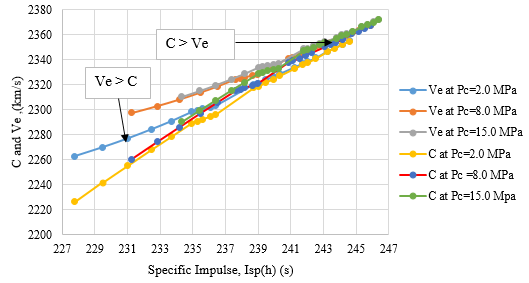
Fig. 6 : Variation of Exhaust velocity across Specific Impulse

??????????????C. Validation of Relationship between Isp(h) and SPC

The formulated mathematical model (12) validates the basic relationship between the SPC and Isp(h) for various chamber pressures in lower atmospheric altitude as shown in Fig 7. The variation is in accordance with the theoretical performance equation of the rocket presented by Sutton G.P, et al., (1983) in his book [1] and validates the relation accordingly in view of higher thrust demands with increasing values of h.

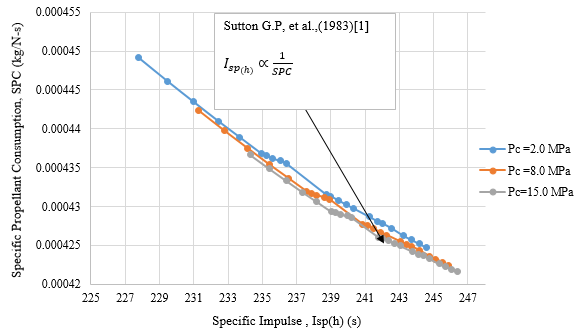
Fig. 7    Relationship between Isp(h) and SPC

???????D. Estimation of Thrust per propellant mass flow rate

Area graph depicted in Fig. 8 with averaged specific impulse (Isp(h)) values for chamber pressures (Pc) ranging from 2.0 to 15.0 MPa (y-axis) and acceleration due to gravity (x-axis) provides an estimate on thrust per propellant mass flow rate across different atmospheric heights. The area under the curve represents the thrust efficiency, offering insights into the propellant's performance under varying altitude conditions. It is observed that as altitude increases, the thrust requirements become higher, which validates the thrust relationship in (9) by demonstrating the dependence of specific impulse on changing gravitational acceleration and ambient pressure with increasing altitude.

???????

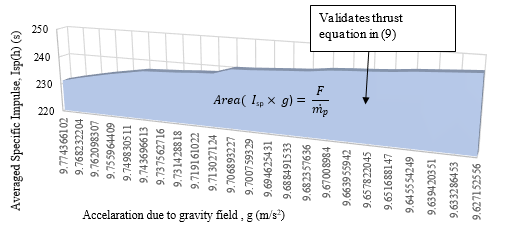Fig. 8   Area curve for Thrust requirement per unit Propellent Mass flow rate

???????E. Inference

The theoretical analysis carried out so far produced convincing results based on the generated simplified theoretical model to compute the ideal specific impulse behaviour of a hybrid propulsion unit across lower atmospheric altitudes. The below Table 3 depicts the inference on performance parameters assessed based on chamber pressure and varying attitudes for fuel C22H46 and N2O oxidizer combination.

Table 3: Averaged Ideal Specific Impulse for Lower Geo-potential Altitudes

Conclusion

The performed theoretical analysis of a pure paraffin wax (n-docosane) and nitrous oxide as oxidizer-based hybrid rocket propulsion system highlights the critical role of ideal specific impulse in achieving the thrust requirements of a hybrid rocket motor at lower atmospheric geo-potential altitudes. While the obtained values are theoretical, practical variations may arise due to factors which include oxidizer-fuel selection and their controllable mixture ratio based on requirements, nozzle geometry and oxidizer-to-fuel proportion adjustments, which has more influence in considering real-time thrust demands and altitude conditions. The findings generated in this work provide valuable insights and serve as a strong motivation to explore the potential of hybrid propulsion systems for future aerospace applications, particularly in altitude operations.

References

[1] G. P. Sutton, Rocket Propulsion Elements, 5th ed. New York, NY, USA: John Wiley & Sons Inc., 1993. [2] P. G. Hill and C. R. Peterson, Mechanics and Thermodynamics of Propulsion, 2nd ed. New York, NY, USA: Addison-Wesley Longman Inc., 1999. [3] R. Mathur and R. P. Sharma, Gas Turbines and Jet and Rocket Propulsion. New Delhi, India: Standard Publishers, 1988. [4] V. Ganesan, Gas Turbines, 2nd ed. New Delhi, India: Tata McGraw-Hill Publishing Co. Ltd., 2003. [5] S. Senthil, Gas Dynamics and Jet Propulsion, 6th ed. Chennai, India: A.R.S Publications, 2009. [6] K. Ramamurthi, Rocket Propulsion, 2nd ed. New Delhi, India: University Science Press, Laxmi Publications Pvt. Ltd., 2016. [7] S. McAllister, J. Chen, and A. C. Fernandez-Pello, Fundamentals of Combustion Process. 2011. [8] Fundamentals of Hybrid Rocket Combustion and Propulsion. Reston, VA, USA: American Institute of Aeronautics and Astronautics, 2007. [9] K. S. Rao, Numerical Methods for Scientists and Engineers, 4th ed. New Delhi, India: PHI Learning Pvt. Ltd., 2021. [10] J. E. Dennis and R. B. Schnabel, Numerical Methods for Unconstrained Optimization and Nonlinear Equations. [Online]. Available: https://doi.org/10.1137/1.9781611971200 [11] S. Mane, “Advancements in Hybrid Rocket Motor Technology: Safety, Performance, and Applications,” Int. J. Enhanced Res. Sci., Technol. Eng., vol. 12, no. 7, pp. 49–51, 2023. [12] V. Siva, “Investigation of Solid Propellant Rocket Engine – A Theoretical Approach,” Int. J. Eng. Res. Appl., vol. 7, no. 9, pp. 73–75, 2023. [13] M. J. Chiaverini, K. K. Kuo, and F. K. Lu, Fundamentals of Hybrid Rocket Combustion and Propulsion, vol. 218, Progress in Astronautics and Aeronautics, Reston, VA, USA: AIAA, 2007. [14] K. Sreehari and M. G. Aswini, “Estimation of Ideal Specific Impulse of Paraffin Wax-Fueled Lab-Scale Hybrid Rocket Motor Using Chebyshev Method,” Int. J. Multidiscip. Res. (IJFMR), vol. 7, no. 1, 2025. [Online]. Available: https://doi.org/10.36948/ijfmr.2025.v07i01.35495 [15] M. T. Migliorino, D. Bianchi, and F. Nasuti, “Numerical Analysis of Paraffin-wax/Oxygen Hybrid Rocket Engines,” in AIAA Propulsion and Energy 2019 Forum, Indianapolis, IN, USA, 2019, Paper 2019-4261. [16] E. W. Lemmon and A. R. H. Goodwin, “Critical Properties and Vapor Pressure Equations for Normal Alkanes and Their Isomers,” J. Phys. Chem. Ref. Data, vol. 29, no. 1, pp. 1–85, 2000. [Online]. Available: https://doi.org/10.1063/1.556054 [17] P. Bose and K. M. Pandey, “Analysis of thrust coefficient in a rocket motor,” Int. J. Eng. Adv. Technol. (IJEAT), vol. 1, no. 3, pp. 30–34, 2012. [18] S. Srivastava, A. Ingenito, and R. Andriani, “Numerical and experimental study of a 230 N paraffin/N2O hybrid rocket,” in Proc. 8th Eur. Conf. Aeronaut. Space Sci. (EUCASS), 2019. [Online]. Available: https://doi.org/10.13009/EUCASS2019-866 [19] H. Lüth, S. C. Nyburg, P. M. Robinson, and H. G. Scott, “Crystallographic and calorimetric phase studies of the N-Eicosane, C20H42: N-Docosane, C22H46 system,” Mol. Cryst. Liq. Cryst., vol. 27, no. 3–4, pp. 337–357, 1974. [Online]. Available: https://doi.org/10.1080/15421407408083141 [20] R. C. Parkinson and S. A. Mace, “On the calculation of thrust coefficient,” Propellants, Explosives, and Rocket Motor Establishment, Report ADA099791, 1981. [21] J. Arves and H. Jones, “A standardized technique for evaluating hybrid rocket motor performance,” in 33rd Joint Propulsion Conference and Exhibit, 1997. [Online]. Available: https://doi.org/10.2514/6.1997-2933 [22] L. Galfetti, L. Merotto, M. Boiocchi, F. Maggi, and L. T. DeLuca, “Experimental investigation of paraffin-based fuels for hybrid rocket propulsion,” Prog. Propulsion Phys., pp. 59–74, 2013. [Online]. Available: https://doi.org/10.1051/eucass/201304059 [23] M. Bouziane, A. E. De Morais Bertoldi, P. Milova, P. Hendrick, and M. Lefebvre, “Development and testing of a lab-scale test-bench for hybrid rocket engines,” in 2018 SpaceOps Conference, 2018. [Online]. Available: https://doi.org/10.2514/6.2018-2722 [24] Manual of the ICAO Standard Atmosphere, 2nd ed. Montreal, QC, Canada: ICAO, 1964. [25] M. C. Tarifa and L. Pizzuti, “Theoretical performance analysis of hybrid rocket propellants aiming at the design of a test bench and a propulsive system,” in EUCASS, 2019. [Online]. Available: https://doi.org/10.13009/EUCASS2019-488 [26] Kalimullah, M. Garg, P. Arun, and F. M. S. Lima, “Motion of a falling object,” arXiv, 2006. [Online]. Available: https://doi.org/10.48550/arXiv.physics/0604106 [27] L. Yaws, Thermophysical Properties of Chemicals and Hydrocarbons. Netherlands: Elsevier Science, 2014.

Copyright

Copyright © 2025 Sreehari Kambrath, Jishnu Thuluvath. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.